I totally agree with Paul Chiusano that the Reactive Manifesto not even wrong. In addition to the breezy non-falsifiability of its assertions, I have trouble with the name itself. Manifestos seldom work out well, in the sense of there not being a lot of corpses. (Plus which, "reactive" is acually a word, and a "reactive manifesto" doesn't sound like it would be very proactive, like.)
BUT reactive programming is important, it's useful, and I need to understand it better. Herewith, then, I shall:
- Very briefly introduce reactive programming as I understand it.
- Complain that I don't understand why they call it Functional Reactive Programming.
- Hazard a guess at what the manifesterati were referring to when they mentioned Finance.
- Build up toy frameworks in Scala and Clojure that seems to me to be truly functional.
Encapsulate the state of the reactive graph in a state monad.Defer discussion of the state monad to the Clojure version.- Show some neat stuff that emerges.
- Conclude that I need to learn Haskell in order to read the academic papers that will show me what I'm not understanding.
Reactive Programming
There's been a lot written on this subject. Martin Odersky gave a whole course (which, fair warning, I did not take), incorporating the concepts introduced in these papers from 2010 and 2012. (Actually, they're sort of the same paper. The later one drops one of the authors, adds some implementation details, but seems to leave out a few useful explanations from the earlier one.) This modified example from the 2010 paper gets the basic point across:
val a = new Var(1)
val b = new Var(2)
val c = new Var(3)
val sum = Signal{ a()+b() }
val result = Signal{ sum() * c() }
observe(result) { x => println(x) }
a()= 7
b()= 35
c()= 1
Not worrying for the moment about how this might work, we expect the above code to print out
27
126
42
as inputs to the Var objects propagate into the calculation maintained by the Signals.
Somewhere, obviously, is a hidden directed acyclic graph (DAG) structure containing directed links between the various objects.
a -----> \
|-----> sum ---->\
b -----> / |----> result
c---->/
There's more to it than this. For example, I've completely ignored discrete Events in time or the ability to
"integrate" over a history of changes. Nonetheless, the illustrated concept, familiar to anyone who's ever
used a spreadsheet, is a valid example of Functional Reactive Programming.
Functional Reactive Programming.
That's what it's called, or FRP for short. The "functional" epithet seems to apply because the you write functions that take input and emit things, while not themselves keeping any internal state. But there's still state! It's just hiding in a giant, global, mutable thingamie whose content we can only infer by doing clever experiments. For concreteness, we'll call the thingamie the DAG or the graph.
When we evaluate a()=7, the 7 is stored in the DAG, along with the new values
of sum and result.
If a, b and c were updated in different threads, with sum
and result consumed in still others, there could be all sorts of fascinating race conditions.
We'll suppose that the authors of the DAG have designed it so as not to crash under
such circumstances, but the system a whole is opaque and certainly stateful.
FRP in Finance
The manifestors have written:
Finance and telecommunication were the first to adopt new
practices to satisfy the new requirements and others have
followed.
Finance comprises many people and many technologies, and there are surely some sophisticated examples of reactivity in the service of Mammon, but the only notable early use of reactivity in the financial sector is a system developed in the mid-90s at Goldman Sachs called secdb. I never worked at Goldman, so everything I say about secdb is hearsay; on the other hand, many people have worked at Goldman, so much has been said and heard (and of course I'm not bound by any sort of confidentiality agreement). Secdb employs a proprietary language called slang (having nothing whatsoever to do with s-lang), which supports a reactive programming style. Since I probably don't know slang, let's pretend its syntax was similar to that of the scala DSL from the Oderksy (et al) papers.
Slang had a twist that they called the "diddle scope" with scope in
sense often delimited by curly braces. Any "diddles" to the DAG
within this scope are undone on exiting it, and the language is
single-threaded, so nobody else can have done anything to the DAG
in the mean time. Pretending that the diddling
is scoped by <<, and that scoping rules are otherwise pythonic,
a = Var(1)
b = Var(2)
sum = Signal{ a()+b() }
<<
b() = 3
diddled = sum()
>>
diddless = sum()
println(diddled,diddless)
would print 4 3.
The phantom DAG here is, in a way, a poor man's persistent data structure. The richer man would have (a) had explicit access to the dag structure, which he would (b) not mutate and restore but rather copy (inexpensively). In fact, one of the key technology figures present at Goldman during the birth of secdb was Neil Sarnak, who, as you can see, did more than dabble in persistent data structures while in academia. I imagine that he would have wanted a true persistent DAG, but the implementations at the time just weren't good enough. Little regarding my fragile ego, Neil did not respond to a groupie-like request for comment.
Today, one could imagine
dag = Dag().set("a",1).set("b",2).set("a","b", _+_)
dag2 = dag.set("b",3)
println(dag2.get("c"), dag.get("c")
printing 4 3, but we'll do better than imagine. In the next section, we'll hack up
a simple reactive framework and show what a fully persistent DAG might buy us.
Would you prefer to continue in Clojure?
A FUNCTIONAL reactive framework in Scala
As usual, the code is github,
with illustrative snippets below. I'll be omitting a few many important nuances,
like dealing with changes to the DAG after its
built, you will and no consideration whatever is paid to performance. As before, there will be Var and Signal
nodes, but we will not be manipulating them directly.
The basic structure of the DAG will be represented by a map of Id[T] to Node[T],
where the latter can be either Var or Signal as in the examples above.
The difference here is that both are immutable case classes with immutable members.
sealed trait Node[T]
case class Id[+T](id:String)
case class Dag(val dag: Map[Id[_],Node[_]])
case class Var[T](deps: Set[Id[T]], value: T) extends Node[T]
case class Signal[T](deps: Set[Id[_]], args: Set[Id[_]], fn: Dag => T,value: Option[T]) extends Node[T]
In both varieties of Node, the deps member, holds Ids of the dependents of
this node, i.e. the nodes that depend on this one. The linkages are via map lookups rather
than conventional references, because we want to hitch a free ride on the the persistent
implementation of immutable.HashMap. Note that, while the Ids are merely labels, they're
still typed by what they're allowed to label.
We will make "assignments" with functions that take one immutable Dag and return another.
def set[T](dag: Dag, id: Id[T], value: T) : Dag // for Var nodes
def set[T](dag: Dag, args: Set[Id[_]], fn: Dag=>T) : Dag // for Signal nodes
Actually, it will be more convenient to implement these as methods of Dag. Here's the first:
implicit def mapToDag(map: Map[Id[_],Node[_]]) = Dag(map)
def set[T](id: Id[T], value :T) : Dag =
dag.get(id) match {
case Some(leaf:Var[T]) => (dag + (id -> leaf.copy(value=value))).sully(id)
case _ => dag + (id -> Var[T](Set[Id[T]](),value))
}
Other than sully, which I'll get to in a minute, the basic logic should be clear.
If there's something there already, we use Map.+ to make a new graph, which
contains a new node that is identical to the old one other than having a different value.
Setting a signal node is a little more complicated, because we need to record our dependency on the arguments of the function:
def set[T](id: Id[T], args: Set[Id[_]],fn: Dag=>T) : Dag = {
val dag2 = dag + (id -> Signal(Set[Id[_]](), args, fn, None))
args.foldLeft(dag2){ (d,i) => d.get(i) match {
case Some(node @ Var(deps,_)) => d + (i -> node.copy(deps=deps+id))
case Some(node @ Signal(deps,__,_,_)) => d + (i -> node.copy(deps=deps+id))
case None => ??? // abort!
}}
}
The foldLeft operation iterates over the argument list, poking our id into every node on
which we depend. Of course we don't actually change any node: at each iteration we just create a new map containing
a new node containing a new set of dependents that now includes us. That's a lot of new maps, so
we're putting a lot of faith in the efficiency of the persistent data structure and the cleverness
of the JVM. (I did warn you that no attention would be paid performance.)
The second argument of foldLeft is a binary function, which in this case uses some relatively fancy
pattern matching and deconstruction. The @ notation allows us to extract both the whole node as well
as the deps within it.
Note also the unpleasant use of ???. We'll get a nasty stack trace if we get to this illegal place.
Now to sully. This function will follow the trail of deps, marking every signal node it finds as
requiring calculation. This technique is often called "dirty bit propagation," so the name of the function
is moderately witty but needlessly obscure. Too late to change it though. "Dirtyness" in our case will be
indicated by the absence of a value, i.e. the Option[T] being None.
def sully(id: Id[_]) : Map[Id[_],Node[_]] = {
dag.get(id) match {
case Some(Signal(_,_,_,None)) => dag // node is already dirty
case Some(s @ Signal(deps,_,_,Some(_))) =>
deps.foldLeft(dag + (id -> s.copy(value=None))) {(d,i)=>d.sully(i) }
case Some(Var(deps,_)) => deps.foldLeft(this.dag)((d,i)=>d.sully(i))
case None => ???
}
}
This is a classic recursive depth first search, except that we're using foldLeft to iterate over children,
and the recursion occurs in the folding function.
Note that the Some(Var) match should occur
exactly once, since only Signal nodes are dependents.
There are only a few more pieces to put in place. The following function will ensure that a node in which we're interested has been calculated:
def ensure(id: Id[_]) : Map[Id[_],Node[_]] = dag.get(id) match {
case Some(Var(_,_)) | Some(Signal(_,_,_,Some(_))) | None => dag
case Some(node @ Signal(_,args,_,None)) => {
val dag2 = args.foldLeft(dag)((d,i)=>d.ensure(i))
dag2 + (id -> node.copy(value=Some(node.fn(dag2))))
}}
This is also a depth first search, but it searches back along the args trail rather than
forward along deps.
When it finds a Signal with a None value, it recurs to ensure all the
arguments are available and then evaluates the function.
Now we need a way to get information out of the graph. Since doing so may trigger a calculation
and in so doing change the graph, our method will return a tuple (Dag,T):
def get[T](id:Id[T]) : (Dag,T) = {
val dag2 = ensure(id)
dag2.get(id) match {
case Some(Signal(_,_,_,Some(v))) => (dag2,v.asInstanceOf[T])
case Some(Var(_,v)) => (dag2,v.asInstanceOf[T])
case _ => ???
}
}
def getv[T](id:Id[T]) : T = get(id)._2
The asInstanceOf[T] coercion is hideous, but I can't see a way around it using
Scala's type system. The declaration of Map[[Id[_],Node[_]] does not ensure
matching Id and Node types, and
type DagMap[T] = Map[[Id[T],Node[T]]
would have restricted the map to holding only one type. I will look into shapeless' heterogeneous maps, which can enforce relationships between the types of keys and values, but I haven't seen any examples were those types were themselves polymorphic.
Before we party, it will be convenient to sugar up the Id class a bit.
case class Id[+T](id:String) {
def this() = this(UUID.randomUUID().toString())
override def toString = id
def apply(implicit dag: Dag) : T = dag.dag.get(this) match {
case Some(Var(_,v)) => v.asInstanceOf[T]
case Some(Signal(_,_,_,Some(v))) => v.asInstanceOf[T]
case _ => ???
}
}
This apply method for retrieving already calculated values
is meant to be used inside signal functions, making them somewhat prettier:
set(c,Set(a,b),{<> => a(<>) + b(<>)})
The <> is a valid Scala identifier that is shorter than dag and stands out better.
Putting it all together,
val a = Id[Double]("a")
val b = Id[Double]("b")
val c = Id[Double]("c")
val dag = new Dag().set(a,2.0).set(b,3.0).
set(c,Set(a,b),{<> => a(<>) + b(<>)})
val dag2 = dag.set(a,5.0)
println("Before valuation:\ndag="+dag+"\ndag2="+dag2)
println("After valuation:\n"+dag.get(c)+"\n"+dag2.get(c))
you can see that we've replicated the example, but without global state or randomly throwing away information:
Before valuation:
dag=Dag(Map(a -> Var(Set(c),2.0), b -> Var(Set(c),3.0), c -> Signal(Set(),Set(a, b),<function1>,None)))
dag2=Dag(Map(a -> Var(Set(c),5.0), b -> Var(Set(c),3.0), c -> Signal(Set(),Set(a, b),<function1>,None)))
After valuation:
(Dag(Map(a -> Var(Set(c),2.0), b -> Var(Set(c),3.0), c -> Signal(Set(),Set(a, b),<function1>,Some(5.0)))),5.0)
(Dag(Map(a -> Var(Set(c),5.0), b -> Var(Set(c),3.0), c -> Signal(Set(),Set(a, b),<function1>,Some(8.0)))),8.0)
A more complicated example
Now a more complicated example, one that is popular when demoing secdb-like systems, but this time with a rich-man's "diddle scope." We'll construct a graph to price a call option using the discredited Black Scholes model:
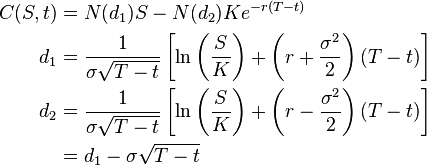
S is a stock price and K is the "strike" ... think of this as some random formula if you like. We can express it in graph form as follows:
def N(x:Double) = (1.0 + Erf.erf(x/Math.sqrt(2.0)))/2.0
val opt = new Dag().
set(K,101.0).
set(S,100.0).
set(T,1.0).
set(r,0.01).
set(sigma,0.35).
set(d1,Set(S,T,K,r,sigma), <> => ((Math.log(S(<>)/K(<>))) + (r(<>)+(sigma(<>)*sigma(<>)/2.0))*T(<>)) /(sigma(<>)*Math.sqrt(T(<>)))).
set(d2,Set(d1,T,sigma), <> => d1(<>) - (sigma(<>)*Math.sqrt(T(<>)))).
set(c,Set(S,T,K,r,d1,d2), <> => S(<>)*N(d1(<>)) - K(<>)*Math.exp(-r(<>)*T(<>))*N(d2(<>)))
Not much going on here, but now for some fun.
It turns out that the derivative $\partial c/\partial S$ is useful to know, as it represents the amount of stock you'd need in order to hedge (exactly counterbalance) fluctuations in the option price. In this simple case, it's easy to take the derivative analytically, but, in general, we might calculate it by finite differencing. In the diddle scope paradigm, that would be accomplished with an unsightly bump and restore, but we can do much better. Let's add a node to the graph:
.set(delta,Set(c,S), <> => (<>.set(S,S(<>)+0.01).getv(c) - c(<>))/0.01)
println(opt.getv(c),opt.getv(delta))
// (13.894175181425787,0.5695720583588582)
The anonymous function is retrieving the current value of S, creating a new graph where it's been increased by 0.01 and extracting c's value reactively. It does this perfectly safely, with no possibility of corrupting the original graph and no need to restore it explicitly. We could even have dispatched the delta calculation to another thread, completely without worry. We get all this, because the graph is just a value!
Rueful Conclusion Never Graduate
I believe that the foregoing could be industrialized, and I can imagine many useful applications. However, I don't know that this is actually new, because I can't understand the literature (for example, this survey) and I can't understand the literature, because it's all in Haskell. It's time to L[M]AHFGG.
(But I promise to post the clojure version first.)
Comments
comments powered by Disqus