In my last post, I talked a bit about how FRP might look if state were maintained explicitly in persistent data structures, rather than in hidden mutable structures. The accompanying code was in Scala, but my first implementation was actually in Clojure. I was originally going to use the Clojure code in the post, but, having taken motivating example code from a Scala paper, it felt lazy to switch to Clojure just because I felt like it.
That said, it really was more fun to write in Clojure, and in some ways I think it is clearer. Additionally, it seems more interesting to take about state monads in Clojure, and state monads are bound to come up when you compose stateful operations.
The code is on github with illustrative snippets below. As in the Scala post, I'll glide over a few details - some (but not all) of which are dealt with properly in the comitted code.
This will all be easier to follow if you've read the previous post at least through the "FRP in Finance" section.
Stop!!!
Have you read the previous post up through the "FRP in Finance" section? The Scala content is minimal, I swear.
Go
Then, starting from here, we'll:
- Set out the basic framework.
- Pretty it up with macros.
- Show how the state monad might fit in but then decide not to use it.
- Illustrate the advantages of a functional approach with an example from finance.
Basic structure
The structure of the directed acyclic graph (the DAG) will be represented in a nested map that looks like this:
{:leafnode {:deps #{:nodethatdepends :anotherone}
:value VALUE }
:nodethatdepends {:function #<somefunctionthing>
:args #{:leafnode}
:dirty TRUEORFALSE}}
We will write functions that:
- Build up the DAG, keeping track of what depends on what and how.
- Propagate the
:dirtyflag through dependends whenever we change a leaf value. - Evaluate the functions at the dirty nodes when we retrieve a value.
The first thing we might like to do is set a leaf value:
(defn set-val [dag k v]
(-> dag
(assoc-in [k :value] v)
(sully k)))
The job of sully is to propagate :dirtyness. We'll get to that in a moment. The main thing
is that it returns the DAG, just like all the standard clojure.core "change" functions, using
the -> macro to thread through operators on it.
Setting a function is almost as easy (though, for the moment, the functions themselves won't be very attractive).
(defn set-fn [dag k kargs dag->val]
(-> dag
(assoc-in [k :args] kargs) ;[1]
(sully k) ;[2]
(assoc-in [k :function] dag->val) ;[3]
(set-deps k kargs))) ;[4]
We store the arguments [1], sully [2]
as necessary (but, again, forget about how that might work for a moment)
and store the function [3]. The purpose of calling
set-deps [4] is to add the keywords in kargs to all
the :deps sets of every node we depend on.
In set-deps, we iterate over the argument list, poking our id into every node on
which we depend. Of course we don't actually change any node: at each iteration we just create a new map containing
a new node containing a new set of dependents that now includes us. That's a lot of new maps, so
we're putting a lot of faith in the efficiency of the persistent data structure and the cleverness
of the JVM. (I did warn you that no attention would be paid performance.)
(defn set-deps [dag kf kargs]
(reduce (fn [dag k] ;[1]
(update-in dag [k :deps] #(if % (conj % kf) #{kf}))) ;[2]
dag kargs)) ;[3]
This is compactly
accomplished by reducing [1] over the kargs, starting with
the original dag [3]
and repeatedly using update-in to conj [2] in the new dependencies.
With these two functions, we can create a primitive DAG:
playground.reactive> (-> {} (set-val :a 3.0)
(set-fn :c [:a :b] (fn [dag] (+ (dag :a) (dag :b)))))
{:c {:function #<reactive$eval10321$fn__10322 playground.reactive$eval10321$fn__10322@5f3acfa8>, :dirty true, :args [:a :b]},
:a {:deps #{:c}, :value 3.0},
:b {:deps #{:c}}}
Both a and b "know" that c is a dependent, so if either changes, we will
know that the latter must too.
Of course this won't do anything yet. There are two additional important functions to add.
First, the aforementioned sully.
This function will follow the trail of :deps, marking every node it finds as :dirty, i.e.
requiring calculation. This technique is usually called "dirty bit propagation," no my nomenclature
isn't inexcusably fanciful.
(defn- sully [dag k]
(if (get-in dag [k :dirty]) dag ;[1]
(let [isfn (get-in dag [k :function])
dag (if-not isfn dag (assoc-in dag [k :dirty] true)) ;[2]
deps (get-in dag [k :deps])]
(reduce sully dag deps)))) ;[3]
This is a classic recursive depth-first-search, except that we're using reduce [3] to
iterate over children, and the recursion occurs in the reduction function.
The search gets truncated [1] if the node is already dirty; otherwise,
we dirty the function nodes [2]. Our reliance on an efficient persistent
map is even greater here than it was for set-deps.
Second, we need something to actually evaluate our functions. This is
also a depth first search, but it searches back along the :args trail,
rather than forward along deps::
(defn- ensure-val
[dag k]
(let [node (get dag k)
dag->val (get node :function)
dirty (get node :dirty)]
(if-not (and function dirty) dag ;[1]
(-> dag ;[2]
(as-> % (reduce ensure-val % (node :args))) ;[3]
(as-> % (assoc-in % [k :value] (dag->val %))) ;[4]
(assoc-in [k :dirty] false))))) ;[5]
If this is not function node or it's not dirty, there's nothing to do here, so
the search stopss [1].
Otherwise, we'll thread [2] dag through some accretions,
first [3] ensuring recursively that any arguments are available,
then [4] evaluating the function and setting its return value in the node,
finally [5] clearing the dirty flag. When all is said and done, we'll
have a DAG from which the value for k may be safely plucked.
Now we need a way to get information out of the graph.
Since the heavy lifting is done by ensure, there's not a lot to this function,
other than remembering to return the new DAG along with the value:
(defn get-val
[dag k]
(let [dag (ensure-val dag k)]
[dag (get-in dag [k :value])]))
Let's play.
(defn pridentity [x] (println x) x) ; useful
(-> {}
(set-val :a 1)
(set-val :b 2)
pridentity
(set-fn :c [:a :b] (fn [dag] (+ (get-in dag [:a :value]) (get-in dag [:b :value]))))
pridentity
(ensure-val :c))
This will create our simple c=a+b graph, printing it out at various stages of construction,
{:b {:value 2}, :a {:value 1}}
{:c {:dirty true, :function #<reactive$eval5874>, :args [:a :b]}, :b {:deps #{:c}, :value 2}, :a {:deps #{:c}, :value 1}}
{:c {:value 3, :dirty false, :function #<reactive$eval5874>, :args [:a :b]}, :b {:deps #{:c}, :value 2}, :a {:deps #{:c}, :value 1}}
first with only the value nodes set, then with the unevaluated/dirty function, and finally after evaluation. (I've truncated the anonymus function name for clarity).
Pretty it up with macros
I really don't like the set-fn line above; its complexity disguises what was really a very simple operation.
Wouldn't it be nice to write (set-fn dag c [a b] (+ a b)) instead? Macros can help.
Let's rename the original version to set-fn* and build a macro around it:
(defmacro set-fn
[dagh k args & forms] ;[1]
(let [kargs (map #(keyword %) args) ;[2]
vs (map (fn [k] `(get-in ~'dag [~k :value])) kargs) ;[3]
bindings (interleave args vs)] ;[4]
`(set-fn* ~dagh ~(keyword k) [~@kargs] ;[5]
(fn [~'dag] (let [~@bindings] ~@forms))))) ;[6]
We will use the Scottish sounding dagh [1] as the macro argument, to distinguish
it from the dag the argument in the function we create.
First [2] we convert an argument vector like [a b] into a list of keywords '(:a :b).
Then [3] for each keyword in that list, we generate the get-in call that
will retrieve the computed value from the nested map.
Clojure macro syntax may look a bit like line noise,
but what's going on here isn't too complicated. The leading backtick in `(get-in ~'dag [~k :value])
quotes the entire s-expression, so get-in and :value get treated as if they appeared in
regular Clojure. The punctuation in ~'dag prevents dag from getting name-space qualified, which
is important, since it's going to be used as function argument. The tilde in ~k just expands it to the corresponding
keyword element of kargs.
Interleaving [4] the arguments and the get-in expressions gives us bindings suitable for
insertion into a let form.
The ~dagh in [5] will expand to the actual argument of the macro; ~(keyword k) turns
c into :c; and we splice in the argument keywords to form [:a :b].
The function itself uses the unqualified ~'dag as an argument, splices in our bindings
from above, and snarfs the function forms as they were written.
Similarly renaming and wrapping the other functions (see the code if you care), lets us do this
(def d1 (-> {}
(set-val a 1)
(set-val b 2)
(set-fn c [a b] (+ a b))))
(def d2 (-> d1 (set-val b 3)))
(println (gv d1 c) (gv d2 c))
and get the expected 3 4.
The state monad
The conclusion of this section is going to be that I can't see much point using the state monad here, so feel free to skip it if anticlimaxes get you down. At the same time, it's not unlikely that I'm wrong about this, and I'd really like someone to tell me why.
So far, we've used the -> threading macro to perform successive operations on the DAG.
We could accomplish the same thing by fmaping together functions that don't refer
to the DAG explicitly in their arguments.
The state monad stores values in closures, specifically in functions from state to a tuple of the value and a potentially different state. So
(fn [dag]
(let [[dag v] (get-val* dag :c)]
[v dag]))
is a monad holding the state-dependent value of the c node of some unspecified DAG.
Now we could write a function to generate one of these functions from an arbitrary symbol k instead of :c:
(defn get-val-s* [k]
(fn [dag]
(let [[dag v] (get-val* dag k)]
[v dag])))
Other than the fact that the thing being returned is a function, this isn't that much different from a function that returns a more straightforward sort of monad, like an option, e.g.
(defn parse-int [s]
(try [:some (Integer/parseInt s)]
(catch Exception e [:none nil])))
Writing similar "something -> state monad" functions for our other DAG operations,
(defn set-val-s* [k val] (fn [dag] [nil (set-val* dag k val)]))
(defn set-fn-s* [k args f] (fn [dag] [nil (set-fn* dag k args f)]))
spiffing them up in macros,
(defmacro set-val-s [k v] `(set-val-s* ~(keyword k) ~v))
(defmacro set-fn-s [k args & forms] `(set-fn-s* ~(keyword k) ~(vec (map keyword args)) (rfn ~args ~@forms)))
(defmacro get-val-s [k] `(get-val-s* ~(keyword k)))
and employing the for comprehension macro from clojure.algo.monads, the earlier example looks like
((m/domonad m/state-m
[_ (set-val-s a 1)
_ (set-val-s b 2)
_ (set-fn-s c [a b] (+ a b))
v (get-val-s c)]
v) {})
That's a bit pointless, since everything but the final result is thrown away, but, now that we're pretty far down the monadic contrivance hole, we could do some more complicated manipulations
((m/domonad m/state-m
[_ (set-val-s a 1)
_ (set-val-s b 2)
_ (set-fn-s c [a b] (+ a b))
v (get-val-s c)
_ (set-val-s a (* v v))
w (get-val-s c)]
(str "got " w)) {})
and we'll find that we "got 11". That's neat, suppose.
A more complicated example, but not with monads
Now a more complicated example, one that is popular when demoing secdb-like systems, but this time with a rich-man's "diddle scope." We'll construct a graph to price a call option using the discredited Black Scholes model:
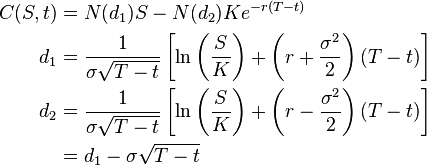
S is a stock price and K is the "strike" ... think of this as some random formula if you like. We can express it in graph form as follows:
(defn N [x] (/ (+ 1.0 (Erf/erf (/ x (Math/sqrt 2.0)))) 2.0))
(defn option []
(-> {}
(set-val K 101.0)
(set-val S 100.0)
(set-val T 1.0)
(set-val r 0.01)
(set-val sigma 0.35)
(set-fn d1 [S T K r sigma] (/ (+ (Math/log (/ S K)) (* (+ r (/ (* sigma sigma) 2)) T)) (* sigma (Math/sqrt T))))
(set-fn d2 [d1 T sigma] (- d1 (* sigma (Math/sqrt T))))
(set-fn c [S T K r d1 d2] (- (* S (N d1)) (* K (Math/exp (* (- r) T)) (N d2)))))
#_(watch this spot))
Not much going on here, other than the usual horror of writing arithmetic expressions in prefix notation, but now for some fun.
It turns out that the derivative $\partial c/\partial S$ is useful to know, as it represents the amount of stock you'd need in order to hedge (exactly counterbalance) fluctuations in the option price. In this simple case, it's easy to take the derivative analytically, but, in general, we might calculate it by finite differencing. In the diddle scope paradigm, that would be accomplished with an unsightly bump and restore, but we can do much better. Let's add a node to the graph:
(set-fn delta [c S] (/ (- (-> dag (set-val :S (+ S 0.01)) (gv c)) c) 0.01 ))
The anonymous function is retrieving the current value of S, creating a new graph where it's been increased by 0.01 and extracting c's value reactively. It does this perfectly safely, with no possibility of corrupting the original graph and no need to restore it explicitly. We could even have dispatched the delta calculation to another thread, completely without worry. We get all this, because the graph is just a value!
Rueful Conclusion Never Graduate
I believe that the foregoing could be industrialized, and I can imagine many useful applications. However, I don't know that this is actually new, because I can't understand the literature (for example, this survey) and I can't understand the literature, because it's all in Haskell. It's time to L[M]AHFGG.
Comments
comments powered by Disqus